Рост и регуляция численности популяцийЭволюционная экология / Принципы популяционной экологии / Рост и регуляция численности популяцийСтраница 1
В конечном мире ни одна популяция не может расти экспоненциально очень долго (рис. 5.8). Раньше или нозже каждая популяция должна столкнуться с неподходящими условиями обитания или с нехваткой ресурсов, необходимых для дальнейшего размножения. Через какой-то длительный промежуток времени, если только средняя фактическая скорость увеличения не равна нулю, любая популяция либо сократится в численности и в конце концов вымрет, либо увеличит свою численность за счет вымирания других популяций. ББас. У нас доступна аренда микроавтобуса на свадьбу с почасовой оплатой. Звоните.
Для начала ограничимся рассмотрением популяций с фиксированными для каждого возраста параметрами (постоянными и mJ. Возрастную специфичность пока не будем учитывать, а. величинам и г позволим изменяться в зависимости от нлотности популяции. Чтобы сделать это, определим предельную плотность насыщения (К), как ту плотность популяции (т. е. число особей на единицу площади), при которой чистая скорость размножения К равна единице, а врожденная скорость увеличения популяции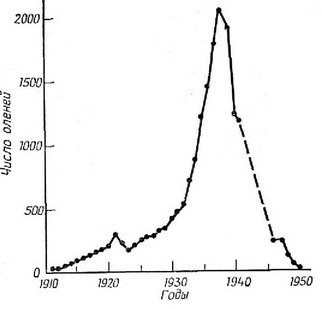 
Рис. 5.8. В 1911 г. на остров Сент-Пол (острова Прибылова, Аляска) бвтло завезено 25 северных оленей. Популяция росла оченв быстро, почти по экспоненте, до 1938 г., когда на острове нло-щадвю примерно 106 км обитало уже более 2000 оленей. В резулв-тате неревынаса была сервезно подорвана пищевая база (главным образом, лишайники), и популяция нотернела крах: в 1950 г. на острове осталосв толвко 8 особей. Подобная носледователвноств со-бытий наблюдаласв и на острове Сент-Метвю в период с 1944 по 1966 г. (Из Krebs, 1972 по дан-HBIM Scheffer.)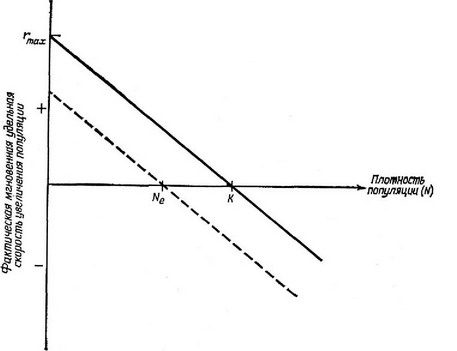 
Рис. 5.9. В соответствии с допущением логистического уравнения Ферхюлвста — Пирла фактическая мгновенная уделвная скороств увеличения нонуляции (г) при возрастании плотности популяции линейно снижается. Сплошная линия соответствует оитималвным условиям, при которвгх разноств между Ь ж (1 мак-сималвна. Прерывистая линия показывает, как снижается фактическая уделвная скороств увеличения популяции с возрастанием N при условии высокой уделв-ной смертности. Равновесная численноств популяции Ж, в последнем случае менвше, чем пределвная плотноств насыщения данной среды К (см. также рис. 5.12).
(г) равна нулю. При «нулевой плотности» (когда присутствует один организм или полностью отсутствует какая-либо конкуренция) Яд максимально и Для любой заданной плотности выше нулевой Кд ш г уменьшаются до тех пор, пока при плотности К популяция не перестанет расти. Популяция, изначально имевшая плотность выше К, сокращается до тех пор, пока не достигнет стационарного состояния или плотности, равной К (рис. 5.9). Таким образом, мы определим г или dN/dt • как фактическую мгновенную скорость увеличения, которая равна нулю в точке, соответствующей К, отрицательна при плотности выше К и положительна, когда плотность популяции ниже К.
Самое простое предположение, которое мы можем сделать, — это допустить, что г линейно уменьшается с ростом и становится равной нулю при Ы=К (рис. 5.9). Это предположение приводит к классическому логистическому уравнению Фепхюльста — Пипла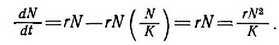 
Член rN (N/K) в уравнении (16) и член zN в уравнении (18) отражают зависимое от плотности снижение скорости увеличения популяпии. Таким образом, при N= 1 («экологический вакуум») dN/dt меняется почти экспопеппиальпо, а при N = K популяпия находится в стапиопарпом состоянии около плотности ее насыщения и dN/dt =0. Логистические уравнения (их существует много помимо уравнения Ферхюльста — Пирла) дают так называемые сигмоидные (S-образпые) кривые увеличения популяпии (рис. 5.10). В логиистическом уравнении Ферхюльста — Пирла безусловны три допущения: 1) все особи эквивалентны, т. е. добавление каждой повой особи при любой плотности уменьшает фактическую скорость увеличения па одну и ту же величину — 1/К (рис. 5.9); 2) величины г и К константы; 3) при изменении фактической скорости увеличения в ответ па изменение N не наблюдается никакой временной задержки. Посколььсу все три допущения па самом деле не реалистичны, логистическое уравнение не раз подвергалось строгой критике (Allee et al., 1949; Smith, 1952, 1963a; Slobodkin, 1962).
Вынеся за скобки, можно переписать уравпепие (16):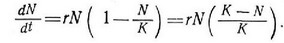 
Или, приняв, что г/К = Z, записать его в следующем виде: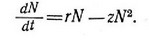 
Смотрите также
Заключение.
Основным критерием экологической политики вообще является ее
действенность. Распространено мнение, что в
экологической сфере наиболее действенным является административный подход, то есть подход рас ...
Введение
Исследований, непосредственно посвященных популяционной структуре вида и закономерностям
динамики численности рыжей полевки, немного, к тому же все они носят региональный
характер и основываются н ...
Понятие исследования
В современном менеджменте исследование является главным фактором успеха, а если выражаться по научному, — главным фактором повышения эффективности управления. Исследование — это не только ...