Рост и регуляция численности популяцийЭволюционная экология / Принципы популяционной экологии / Рост и регуляция численности популяцийСтраница 2
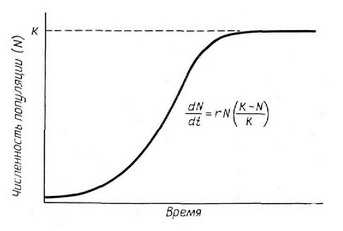
Рис. 5.10. График роста популяции, происходящего в соответствии с логистическим уравнением Ферхюлвста — Пирла, представляет собой 8-образную кривую, выходящую на плато при так называемой пределвной плотности насыщения К. Плотноств развивающейся популяции, если ее началвная плотноств бвша вы-ше К, уменвшается по экспоненте до величины К, которая представляет собой, таким образом, единственно возможное устойчивое равновесие. 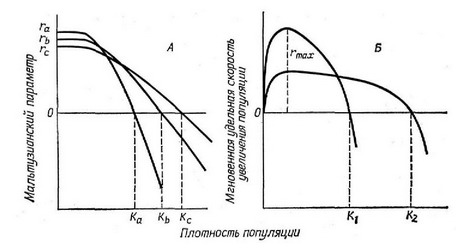
Рис. 5.11. Гипотетические криволинейные зависимости мгновенной скорости увеличения популяции от плотности. Возможны также и вогнутые кривые.
Более правдоподобные нелинейные зависимости скорости увеличения от плотности популяпии показаны па рис. 5.11.
Обратите внимание, что зависимые от плотности изменения рождаемости и смертности объединены использованием показателя г (далее эти изменения будут рассмотрены по отдельности). Предельная плотность насыщения также исключительно сложное и не всегда ясное понятие, так как оно во многом зависит от обеспеченности возобновляемыми и невозобновляемыми ресурсами, которые сами по себе являются переменными величинами. Для подавляющего большинства организмов плотность насыщения широко варьирует в зависимости от места и момента времени. Существует также неизбежное запаздывание в цепи обратной связи между плотностью популяции и фактической мгновенной скоростью ее увеличения. С учетом всех указанных допущений могут быть разработаны более реалистические уравнения, однако при этом быстро возрастает сложность используемого математического аппарата, что затрудняет его применение. Тем не менее целый ряд популя-ционных явлений может быть хорошо проиллюстрирован простым логистическим уравнением Ферхюльста—Пирла, и его необходимо отчетливо понимать, чтобы разобраться в таких же простых уравнениях конкуренции Лотки—Вольтерра, рассматриваемых в гл. 6. Следует, однако, признать многочисленные недостатки логистического уравнения, которое может быть использовано только в качестве первого приближения для описания незначительных кратковременных изменений в росте популяции, находящейся вблизи состояния равновесия (т. е. в том случае, когда зависимость приближается к линейной).
Обратите внимание на то, что в логистическом уравнении (16) г — это на самом деле Уравнение можно разрешить относительно фактической скорости увеличения х, которая представляет собой переменную величину, зависящую от г, JV и к, разделив правую и левую части па N:
dN / — / N \
Фактически мгповеппая удельная скорость увеличения популяции, г, всегда мепьще или равна г (г в логистическом уравнении). Как следует из уравнения (19) и рис. 5.9, г линейно уменьшается с увеличением плотности, что является допущением логистического уравпепия Ферхюльста—Пирла.
Фактическая мгновенная удельная скорость увеличения популяции (гJ включает в себя два компонента: фактическую мгпо-веппую удельную рождаемость (скорость рождаемости) b и фактическую мгновенную удельную смертность (скорость смертности) а. Разность между b vi с1, т. е. (b—d),— это и есть г. При воображаемых идеальных условиях, когда значение b максимально, а d мипимальпо, г достигает своей паибольщей величины, равной "max- Согласно логистическому уравпепию, подобное положение реализуется при мипимальпой плотности или в условиях «полного конкурентного вакуума». Для большей точности обозначим величины h и d индексом, показывающим, что эти величины зависят от плотности. Тогда Ь—= (которая представляет собой величину при плотности а Ьд—dg= г. Когда = величины г и dN/dt равны пулю, а популяция находится в состоянии равповесия. На рис. 5.12 показано, как в соответствии с логистическим уравнением й и й? линейно зависят от N. При любой заданной плотности значения и d определяются липейпыми уравнениями:
Ь, = bg-xN, (20)
= d„+yN, (21)
где X и у — углы наклона прямых па рис. 5.12 (см. также Bartlett, 1960; Wilson, Bossert, 1971). Мгповеппая смертность d, очевидно, характеризуется как зависимыми, так и пезависимыми от плотности компонентами. В уравпепии (21) и на рис. 5.12 величина yN измеряет компонент d, зависимый от плотности, а — независимый. При равповесии Ь, должно равняться й?
b„-xN =d„ + yN. (22)
Обозначив N в условиях равповесия через N, а разность (b—dj через г и произведя некоторые преобразования, получим
г = (x+y)N„ (23)
или 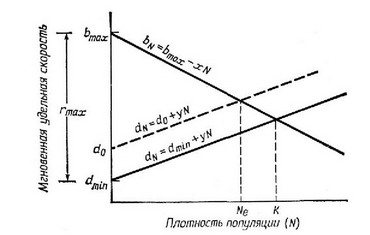
Смотрите также
Введение
Исследований, непосредственно посвященных популяционной структуре вида и закономерностям
динамики численности рыжей полевки, немного, к тому же все они носят региональный
характер и основываются н ...
Основные функции и принципы экологической политики.
Комплексный характер экологических проблем
требует комплексного государственного управления в области охраны окружающей
среды. Ниже перечислим функции такого управления.
* Экологическое
прогно ...
Морфофункциональные особенности лейкоцитов млекопитающих, разводимых в неволе
в условиях европейского севера
Представлены данные о морфофункциональных особенностях лейкоцитов крови различных
видов животных из отряда Carnivora— норок, песцов, лисиц и енотовидных собак, разводимых
в неволе в условиях Карел ...