Уравнение Лотки — Вольтерра и теория конкуренцииЭволюционная экология / Взаимодействия между популяциями / Уравнение Лотки — Вольтерра и теория конкуренцииСтраница 1
Около 50 лет назад Лотка (Тоїка, 1925) и Вольтерра (УоИегга, 1926, 1931) поставили изучение конкуренции на сравнительно прочную, хотя и весьма упрощенную теоретическую основу. Их Уравнения конкуренции сильно повлияли на развитие современной экологической теории и представляют собой хороший пример математической модели важного экологического явления. Кроме того, эти уравнения повлекли за собой разработку нескольких Других очень полезных понятий, которые концептуально от них не зависят (понятия коэффициентов конкуренции, матриц сообщества и диффузной конкуренции).
Уравнения конкуренции Лотки — Вольтерра представляют собой видоизменение логистического уравнения Ферхюльста— Пирла (гл. 5) и основываются на одинаковых допущениях. Рассмотрим два конкурирующих вида, характеризующиеся величинами плотности и и имеющие в отсутствие друг друга предельную плотность насыщения К или К. Каждому виду присуща таьсже своя максимальная мгновенная удельная скорость увеличения: г и г. Одновременное увеличение численности двух обитающих вместе и конкурирующих видов описывается парой дифференциальных логистических уравнений: 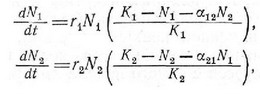
где а„ и а — коэффициенты конкуренции; а„ — характеристика вида 2, которая отражает меру его конкурентного давления па одну особь популяции вида 1; а — апалогичпая характеристика вида 1, отражающая меру его давления на вид 2. Индексы при коэффициентах конкуренции сразу показывают, какая из популяций испытывает влияние и какая его оказывает. Например, а„ — степень подавляющего действия одной особи вида 2 на рост популяции 1, а а — степень подавляющего действия одной особи вида 1 на популяцию вида 2. В отсутствие межвидовой копкурен-ции или равны нулю в уравнении (1); а или равны нулю в уравнении (2)] рост обеих популяций описывается сигмо-идпой кривой, в соответствии с логистическим уравпением Ферхюльста — Пирла; эти нонуляции достигают равновесной величины на уровне предельной плотности насыщения.
По определению подавляющее влияние каждой особи вида 1 на рост своей собственной популяции равно (см. также гл. 5); точно так же подавляющее влияние каждой особи вида 2 на рост своей популяции. Из уравнений (1) и (2) вытекает, что подавляющее влияние каждой особи вида 2 на популяцию вида 1 равно а такое же влияние каждой особи вида 1 на популяцию вида 2 равно а/К. Как правило, хотя и не всегда (см. ниже), величины коэффициентов конкуренции бывают мень-ще 1. Исход конкуренции зависит от относительных величин К, К, а„ и а. Различные комбинации значений этих копстант дают четыре возможных варианта конкурентного взаимодействия (табл. 6.2).
Чтобы убедиться в этом, попробуем выяснить, при какой плотности особей вида 1 плотность вида 2 будет равна нулю и наоборот. Другими словами, какой должна быть плотность каждого вида, чтобы другой вид не имел возможности увеличивать свою численность?
Таблица 6.2. Четыре возможных случая конкуренции, следующие из уравнений конкуренции Лотки—Вольтерра 
Следовательно, в отсутствие другого вида численность обеих популяций увеличивается при любой плотности, если она ниже собствеппой плотности пасыщепия и уменьшается при любом значении, превышающем эту предельную плотность насыщения. В соответствии с изложеппым если в популяции 2 присутствуют особи вида 1, имеющие плотность то уменьшается при всех значениях, а если в популяции 1 присутствуют особи вида 2, имеющие плотность К/а,, то при любой плотности падает. 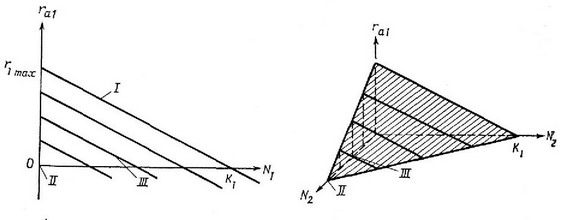
Рис. 6.1. Два графика, показывающие, как в соответствии с уравнениями конкуренции Лотки—Волвтерра фактическая мгновенная уделвная скороств увеличения (rj) зависит от плотности собственной нонуляции {ND и плотности популяции конкурента (N). А. Двухмерный график с четырвмя нрямыми, каждая из которых характеризует определенную плотноств конкурентов (ср. с рис. 5.9), В. Трехмерный график с осью N и плоскостью, на которой лежат все 4 прямые графика А. Плоскоств выходит за иределы значений плотностей Nj и N превышающих Kj и Kj/aj,j соответственно, но здесв rj принимает отрицателвпые значения (ср. с А), /—без конкурентов; II — плотноств конкурентов К/а;, III— плотноств конкурентов 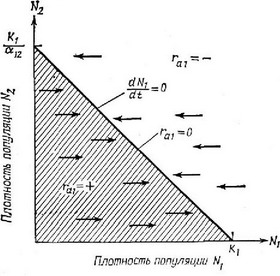
Смотрите также
Структура сообщества
За исключением краткого рассмотрения биомов в гл. 3, до сих пор мы касались только
экологии особей и популяций. В этой главе речь пойдет об экологии сообществ. Подобно
тому как популяции обладают ...
Биогеография
Основная цель экологии состоит в том, чтобы понять те разнообразные факторы,
которые влияют на распределение и обилие животных и растений (Andrewartha, Birch,
1954; Krebs, 1972; Mac-Arthur, 1972). ...
Биологические опасности, связанные с пищей
Научно-технический прогресс сильно повлиял на сферу производства продуктов питания. Технологическая обработка продуктов, консервирование, рафинирование, длительное и неправильное хранение резко снизил ...