• Главная
• Новое
• Популярное
• Поиск
• Карта
• Связь

Уравнение Лотки — Вольтерра и теория конкуренции

Эволюционная экология / Взаимодействия между популяциями / Уравнение Лотки — Вольтерра и теория конкуренции

Страница 2

Рис. 6.2. График, почти полностью совпадающий с графиком на рис. 6.1,5. Отличие состоит лишь в том, что плоскость —здесь изображена нри равном нулю. Все точки, расноложеннвге на прямой, соответствуют равновесию (с1Мус11 = 0), прш котором популяция 1 только самоподдерживается (г =0). В заштрихованной области, расположенной ниже этой прямой, г имеет положительные значения и популяция 1 увеличивается (стрелки направо); ввгше изо-клинв1 г всегда имеет отрицательные значения, и популяция 1 уменьшается (стрелки налево). На этих осях можно ввгчертить такой же график для нонуляции конкурента 2, с той лишь разницей, что точки пересечения изоклины для (ёМ,/111 = 0) будут равнв! К и Куа,, а стрелки расположатся параллельно оси а не оси М,. См. также рис. 6.3.

Вспомним, что по логистическому уравпепию Ферхюльста — Пирла с увеличением N липейпо уменьшается г и при плотности К достигает своего нулевого значения (см. рис. 5.9). Точно такое же соотношение сохраняется в уравнениях конкуренции Лотки — Вольтерра, если не считать того, что в последнем случае семейство прямых связывает г с К и г с К а каждая прямая относится к определенной величине плотности популяции конкурирующего вида (рис. 6.1, А и Б).

Па рис. 6.2 ось г отсутствует, а М отложено против М Таким образом, каждой точке на плоскости М — М соответствует определенное соотношение двух видов и различные плотности их популяций. Приравнивая с к нулю и решая уравпепия (1) и (2), можно найти уравнения для крайних условий уменьшения или увеличения каждой популяции: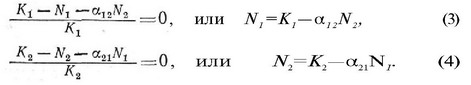

Эти линейные уравнения в графической форме представлены на рис. 6.3. Для каждого вида по ним вычерчены изоклины.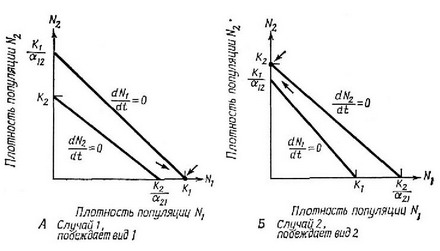

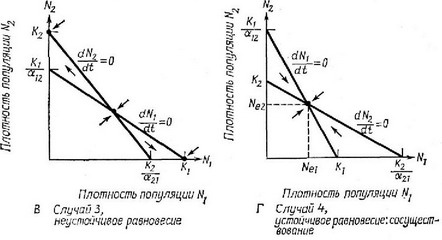
Рис. 6.3. Графики, аналогичные изображенным на рис. 6.2, Отличие состоит лишь в том, что изоклины обоих видов совмещены. А. Случай 1. Изоклина М лежит вышє изоклины и в конкуренции всегда побеждает вид 1. Единственная точка устойчивого равновесия характеризуется координатами = К ж Б. Случай 2. Доминирующим конкурентом является вид 2, который всегда вытесняет вид 1. Здесв устойчивое равновесие наблюдается ири и N, = 0. В. Случай 3. Каждый вид способен сдерживать рост другого (табл. 6.2), т. е. каждый вид подавляет рост популяции другого вида в болвшей степепи, чем рост собственной популяции. Существуют три точки равновесия, но совместное равновесие обоих видов (в точке пересечения двух изоклин) неустойчиво. Две точки устойчивого равновесия имеют координаты и N=0, и N=0. В зависимости от соотношения началвных плотностей победа в копкурепции принадлежит либо одному, либо другому виду. т. Случай 4. Ни один из видов не способен сдерживатв рост другого, но каждый подавляет рост собственной популяции в болвшей степени, чем рост другой. Существует толвко одна точка равновесия, имеющая координаты и Виды могут сосуществовать, при этом плотноств каждого из них должна бытв ниже его иределвной плотности пасыщепия.

Ниже изоклин популяция каждого вида увеличивается, выше— уменьшается. Следовательно, эти линии соответствуют равновесной плотности популяций или величине насыщения. Ни один из видов данной пары не может увеличивать свою плотность, если точка лежит выше его изоклины.

Четыре случая конкурентного взаимодействия, приведенные в табл. 6.2, графически показаны на рис. 6.3. К устойчивому равновесию двух видов приводит лишь одно-единственное сочетание значений — случай 4. Этот вариант возникает тогда, когда ни один из видов не способен достигнуть достаточно высокой плотности, чтобы вытеснить другой, т. е. если одновременно KjKK/a, и В этих неравенствах определены условия сосушество-вания: каждая популяция должна подавлять свой собственный рост в большей степени, чем она подавляет рост своего конкурента. Нри этом если К=К2, то величины а,2 и а, должны быть меньше 1. Когда предельные плотности насыщения не равны, а и а, могут принимать значения больше 1; в этом случае сосуществование будет возможно до тех пор, пока произведение двух коэффициентов конкуренции меньше 1 {(Xj (X2J<\), а отношение К/К находится в пределах и l/aj (см. MacArthur, 1972). Нри совместном равновесии размер каждой популяции (Nj и N) меньше, чем соответствующая величина предельной плотности насыщения каждого вида (К, или К;, рис. 6.3, Д). Таким образом, в условиях конкуренции ни одна из популяций не достигает такой высокой плотности, которой она может достичь в отсутствие конкуренции. Остальные три случая не приводят к устойчивому сосуществованию двух популяций и поэтому представляют меньший интерес. Впрочем, в случае 3 наблюдается неустойчивое равновесие, при котором каждый вид подавляет скорость роста другого вида больше, чем свою собственную. Здесь исход конкуренции полностью зависит от начальных соотношений двух видов.