Теория: колебания хищник — жертваЭволюционная экология / Взаимодействия между популяциями / Теория: колебания хищник — жертваСтраница 1
Теория хищничества во многих отношениях отстала от теории, конкуренции. Возможно, трудности моделирования процесса хищник—жертва связаны с его асимметрией. Лотка (Lotka, 1925)
и Вольтерра (Volterra, 1926, 1931) предложили простую пару уравнений хищничества: 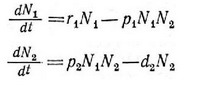
где Nj — плотность популяции жертвы; JV — плотность популяции хищника; — удельная мгновенная скорость увеличения популяции жертвы; й? —удельная скорость гибели популяции хищника; Pj я р — константы хищничества. Каждая из популяций ограничена другой, а эффекты плотности, приводящие к самоограничению, отсутствуют (т. е. отсутствуют члены второго порядка N/ или N/). Таким образом, в отсутствие хищника популяция жертвы растет экспоненциально, а скорость ее увеличения потенциально не ограничена. Произведение плотностей двух видов (NjNJ отражает число контактов между ними; после умножения на константу р этот член становится максимальной скоростью увеличения популяции хищника (pNjNJ. Тот же самый член, умноженный на константу Pj, имеет знак минус в уравнении жертвы и отражает уменьшение скорости роста популяции жертвы.
Уравнения решаются, если приравнять dN/dt к нулю, сократить соответствующие N для получения фактической скорости роста и приравнять г к нулю. Эти алгебраические преобразования показывают, что популяция жертвы достигает равновесной плотности, когда плотность хищника равна г/р{, сходным образом и популяция хищника находится в равновесии при плотности жертвы, равной d/p (рис. 6.16). Следовательно, изоклина каждого вида 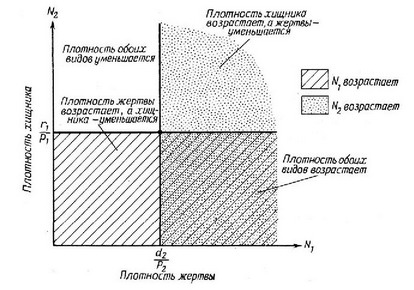
Рис. 6.16. Изоклины хищника и жертвы, построенные по уравнению Лотки-Волвтерра (объяснения см. в тексте).
соответствует какой-то определенной (постоянной) плотности другого вида, и опять-таки при этом отсутствует член, отражающий самоограничение, как, например, в уравнениях конкуренции. Ниже определенной пороговой плотности жертвы плотность хищника всегда уменьшается, а выше — увеличивается; точно так же и плотность жертвы растет, если плотность хищника меньше определенного порога, и уменьшается, если она больше его (рис. 6.16). Совместное равновесие наблюдается в точке пересечения двух изоклин, но плотности жертвы и хищника не сходятся к этой точке. Вместо этого возникают колебания определенной величины, характер которых зависит от начального соотношения плотности хищника и жертвы. Если начальные плотности близки к точке совместного равновесия, то возникают повторяющиеся колебания с низкой амплитудой, если далеки от нее — колебания имеют большую амплитуду. Таким образом, пара упомянутых дифференциальных уравнений имеет периодическое решение, а плотности популяций хищника и жертвы меняются циклически и не совпадают по фазе во времени. Амплитуда колебаний зависит от начальных условий. Система таких повторяющихся незатухающих колебаний в математике называется нейтрально-устойчивой. В биологическом мире нейтральной устойчивости, по-видимому, не существует, поскольку большинство особей и популяций сталкиваются либо с саморегуляцией, либо с обратной связью зависимости от плотности.
Введение в уравнение жертвы простого члена, учитывающего самозатухание (—zN/), означает либо быстрое приближение к равновесию, либо затухание колебаний, что в обоих случаях в конце концов ведет к совместному равновесию (рис. 6.17). В урав 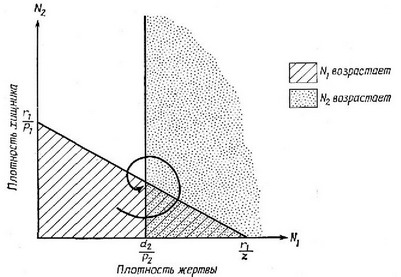
Рис. 6.17. Изоклины хищника и жертвы, иллюстрирующие самозатухающие колебания численности популяции жертвы. Плотности популяций стремятся к состоянию устойчивого совместного равновесия.
нении хищника член, обозначающий самозатухание, должен включать плотность жертвы, так как от нее зависит величина предельной плотности насыщения хищника. Наверное, более реалистичной (хотя и трудно трактуемой математически) простой парой уравнений, моделирующих взаимодействие хищник — жертва, будет следующая: 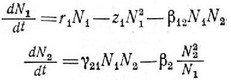
Уравнение жертвы — это простое уравнение конкуренции Лотки — Вольтерра (7), но уравнение хищника имеет новую особенность — конкурентное подавление популяции хищника теперь является функцией относительных плотностей хищника и жертвы. Иначе говоря, подавление популяции хищника усиливается с увеличением плотности хищника и уменьшением плотности жертвы. Заметим также, что популяция хищника не может увеличиваться, если в системе нет некоторого количества жертвы. Однако, несмотря на то что в этой паре уравнений учтены недостатки предыдущих пар, уравнения все же остаются нереалистичными по крайней мере в одном важном отношении. Вообразим ситуацию, при которой численность жертвы превышает количество, которое популяция хищника может уничтожить. В этом случае скорость увеличения популяции хищника не может быть просто пропорциональна произведению двух плотностей, как это записано в уравнении (14), — необходимо принять в расчет пороговые эффекты. В уравнениях, подобных упомянутым, полностью упущены многие важные тонкости взаимодействия хищник — жертва. Например, Соломон (Solomon, 1949) различал два разных способа реагирования хищника на изменение плотпости жертвы. Во-первых, при увеличении плотпости жертвы до определенного предела количество особей жертвы, пойманных и съеденных отдельными хищниками в единицу времени, возрастает. После достижения порога насыщения число съеденных жертв становится более или 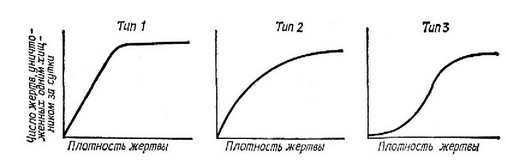
Смотрите также
Введение
Исследований, непосредственно посвященных популяционной структуре вида и закономерностям
динамики численности рыжей полевки, немного, к тому же все они носят региональный
характер и основываются н ...
Экономические методы охраны окружающей среды и особенности их использования в России
Проблема защиты экологии встала перед
человечеством сравнительно недавно. Но уже в нашем веке, который ознаменовал
себя масштабным истощением природных ресурсов, огромным количеством вредны ...
Влияние низкотемпературного закаливания на протеолитическую активность и содержание
фотосинтетических пигментов в листьях проростков озимой пшеницы
На проростках озимой пшеницы (Тп11сит aestivum 1.) изучена динамика активности
амидаз, цистеиновых про-теиназ, а также содержания фотосинтетических пигментов при
холодовом (4°С) закаливании. Показ ...