• Главная
• Новое
• Популярное
• Поиск
• Карта
• Связь

Популяции

Книги по екологии / Общая экология / Популяции

Страница 35

Рис. 142.

Гребневик мнемиопсис – внешний вид (из И. Е. Виноградова и Э. А. Шукшиной, 1993)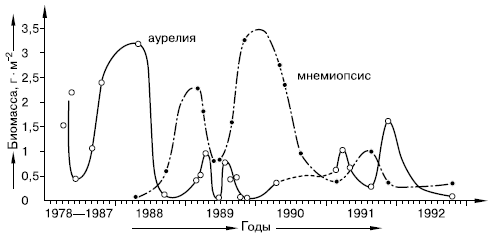

Рис. 143.

Колебания биомассы аурелии и мнемиопсиса в глубоководной части Черного моря (в пересчете на углерод, по И. Е. Виноградову и Э. А. Шукшиной, 1993)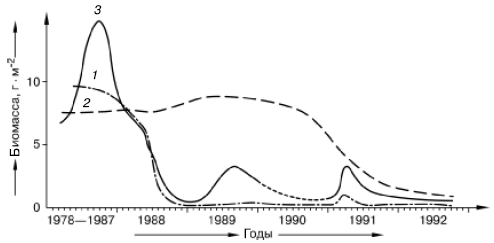

Рис. 144.

Колебание биомассы в открытых районах Черного моря некоторых групп планктонных организмов, которыми питается мнемиопсис (по И. Е. Виноградову и Э. А. Шукшиной, 1993): 1– саггиты; 2 – веслоногий рачок Calanus luxinus; 3 – мелкие рачки и личинки донных животных

Чрезмерное усиление пресса хищников на популяцию какого-либо вида в сообществе может отозваться через сеть трофических зависимостей на довольно далеких уровнях. Например, можно выстроить цепь причинных связей между усилением промысла минтая и других рыб в районе Берингова моря и исчезновением зарослей прибрежных водорослей – ламинарий. Усиленный рыбный промысел (при котором человек выступает в роли мощного хищника) стал одной из причин падения численности питающихся рыбой сивучей и нерпы – основной добычи крупных хищных дельфинов – косаток. С 1991 г. косатки стали охотиться в прибрежных водах на каланов, на которых не нападали раньше, добывая пищу в открытом океане. С начала 90-х годов на Алеутских островах исчезло 40 тыс. каланов, являющихся заповедным видом. Численность этих зверей за 7 лет сократилась почти в 10 раз. Каланы питаются в основном морскими ежами, обилие которых в результате возросло тоже на порядок величин. Морские ежи – главные враги бурых водорослей, заросли которых у побережья сократились за 10 лет в 12 раз.

8.6.6. Математическое моделирование в экологии

Надорганизменные системы, которые изучает экология – популяции, биоценозы, экосистемы, – чрезвычайно сложны. В них возникает множество взаимосвязей, сила и постоянство которых непрерывно меняются. Одни и те же внешние воздействия могут привести к различным, иногда прямо противоположным результатам, в зависимости от того, в каком состоянии находилась система в момент воздействия.

Предвидеть ответные реакции системы на действие конкретных факторов можно лишь через сложный анализ существующих в ней количественных взаимоотношений и закономерностей. В экологии поэтому широкое распространение получил метод математического моделирования

как средство изучения и прогнозирования природных процессов.

Суть метода заключается в том, что с помощью математических символов строится абстрактное упрощенное подобие изучаемой системы. Затем, меняя значение отдельных параметров, исследуют, как поведет себя данная искусственная система, т. е. как изменится конечный результат.

Модели строят на основании сведений, накопленных в полевых наблюдениях и экспериментах. Чтобы построить математическую модель, которая была бы адекватной, т. е. правильно отражала реальные процессы, требуются существенные эмпирические знания. Отразить все бесконечное множество связей популяции или биоценоза в единой математической схеме нереально. Однако, руководствуясь пониманием, что в надорганизменных системах имеется внутренняя структура и, следовательно, действует принцип «не все связи существенны», можно выделить главные связи и получить более или менее верное приближение к действительности.

В построении математических моделей сложных процессов выделяются следующие этапы.

1. Прежде всего, те реальные явления, которые хотят смоделировать, должны быть тщательно изучены: выявлены главные компоненты и установлены законы, определяющие характер взаимодействия между ними. Если неясно, как связаны между собой реальные объекты, построение адекватной модели невозможно. На этом этапе должны быть сформулированы те вопросы, ответ на которые должна дать модель. Прежде чем строить математическую модель природного явления, надо иметь гипотезу о его течении.

2. Разрабатывается математическая теория, описывающая изучаемые процессы с необходимой детальностью. На ее основе строится модель в виде системы абстрактных взаимодействий. Установленные законы должны быть облечены в точную математическую форму. Конкретные модели могут быть представлены в аналитической форме (системой аналитических уравнений) или в виде логической схемы машинной программы. Модель природного явления есть строгое математическое выражение сформулированной гипотезы.

3. Проверка модели – расчет на основе модели и сличение результатов с действительностью. При этом проверяется правильность сформулированной гипотезы. При значительном расхождении сведений модель отвергают или совершенствуют. При согласованности результатов модели используют для прогноза, вводя в них различные исходные параметры.

Следует, однако, отметить, что сама по себе математическая модель не может служить абсолютным доказательством правильности той или иной гипотезы, так как может оказаться, что разные гипотезы приводят к сходным результатам, но она служит одним из путей анализа реальности.