• Главная
• Новое
• Популярное
• Поиск
• Карта
• Связь

Структура и динамика популяций

Книги по екологии / Экология / Структура и динамика популяций

Страница 11

Миграция, или расселение, так же как и внезапное снижение скорости размножения, может способствовать уменьшению численности популяции. Расселение может быть связано с определенной стадией жизненного цикла, например с образованием семян. Рассматривая вопрос об оптимальных размерах популяции в данной среде, следует учитывать поддерживающую емкость или кормовую продуктивность среды. Чем выше поддерживающая емкость, тем больше максимальный размер популяции, который может существовать неопределенно долгое время в данном местообитании. Дальнейшему росту популяции будут препятствовать один или несколько лимитирующих факторов. Это зависит от доступности ресурсов для данного вида.

Таким образом, скорость роста популяции в естественных местообитаниях будет зависеть от климатических изменений, от снабжения пищей и от того, ограничено ли размножение определенным временем года и др., что должно учитываться при составлении моделей или их усовершенствовании.

Математические модели экспоненциального роста популяций и роста при ограниченных ресурсах. Рост численности популяции в геометрической прогрессии можно описать с помощью простых уравнений. Так, в популяции с исходной численностью в N особей за промежуток времени Dt появляется DN новых особей. Если число вновь появившихся особей прямо пропорционально N и Dt, то имеем уравнение DN = r ×Dt ×N. Разделив обе его части на Dt, получим

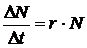(9.4)

Величина 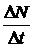- абсолютная скорость роста численности,

г — биотический потенциал или удельная скорость роста численности.

За малый промежуток времени изменение численности равно ее производной 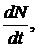и уравнение (9.4) можно переписать так:

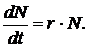(9.5)

Решение этого уравнения — функция

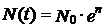. (9.6)

Здесь е — основание натуральных логарифмов (е » 2,72 .). График этой функции и есть экспонента (рис. 9.10,вверху).

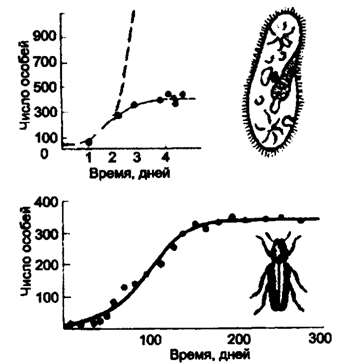
Рис. 9.10. Реальная и теоретическая кривые роста численности инфузорий-туфелек (вверху) и рост численности жуков определенного вида в культуре (численность меняется по правилам логистического роста)

Пунктирная линия — теоретическая кривая (экспонента); сплошная линия — в реальной культуре рост численности замедляется и через определенное время останавливается

В модели экспоненциального роста удельную рождаемость b и удельную смертность d можно обозначить как .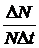

При этом в замкнутой популяции

DN » b×N×Dt - d×N×Dt;

r = b – d. (9.7)

Если смертность выше рождаемости, то убывание численности тоже описывается уравнением (9.6), но с отрицательным г. Такой процесс называют экспоненциальным затуханием численности.

Модель динамики численности популяции при органиченных ресурсх предложил в 1845 г. французский математик Ферхюльст. Уравнение, которое носит его имя, выглядит так:

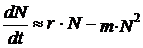(9.8)

Уравнение Ферхюльста отличается от уравнения экспоненциального роста тем, что в правой его части добавляется выражение mN2. Это выражение учитывает число встреч животных, при которых они могут конкурировать за какой-либо ресурс: вероятность встречи двух особей пропорциональна квадрату численности (точнее, плотности) популяции. У многих животных рост численности популяции действительно ограничивается именно частотой встреч особей.